Cálculo do Retorno de um Investimento: Exercício
Cálculo do Retorno de um Investimento: Exercício
Vamos fazer um exercício para calcular o retorno de um investimento fictício. Suponha um investimento mensal em um produto de renda fixa. Nesse investimento, será aportada inicialmente a quantia de R$ 100.000,00.
O investimento será remunerado à uma taxa constante de 0,9% ao mês, juros compostos. Serão feitos aportes mensais no valor de R$ 2000,00, todos os meses sem falta.
Pede-se: Calcular e montar uma tabela mostrando a evolução desse investimento mês a mês, com os montantes calculados durante um período de 10 anos.

Para calcular a evolução desse investimento ao longo de 10 anos com aportes mensais, usando a taxa de juros compostos de 0,9% ao mês, podemos fazer os cálculos mensais para determinar o saldo acumulado mês a mês. Vamos montar a tabela com o resultado desses cálculos, baseado portanto nesses valores:
- Investimento Inicial: R$ 100.000,00
- Aporte Mensal: R$ 2.000,00
- Taxa de Juros Compostos: 0,9% ao mês
A fórmula que usaremos para calcular o saldo acumulado após um período de tempo usando juros compostos é:
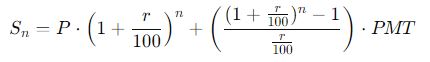
Onde temos:
- Sn é o saldo acumulado após n períodos (meses, neste caso)
- P é o investimento inicial
- r é a taxa de juros mensal
- n é o número de períodos
- PMT é o aporte mensal
Observação: Neste exemplo temos aportes mensais a serem considerados no cálculo. Para calcular o retorno de um investimento único, sem aportes, o método e a fórmula são distintos, e veremos em outros exercícios como fazer isso.
O cálculo pode ser feito usando-se uma planilha de cálculos, como o Microsoft Excel ou o Libre Office, ou ainda usando uma calculadora financeira como a HP 12C. Neste caso, como queremos visualizar a evolução mês a mês, o uso de uma planilha é altamente recomendado, pela facilidade e simplicidade em mostrar os resultados tabulados.
Após realizar o cálculo para cada mês, vamos montar a tabela até completar os 10 anos (120 meses). Porém, vou mostrar apenas os primeiros e últimos meses calculados, para não deixar a tabela longa demais aqui (ou seja, vou truncar a tabela):
| Mês | Investimento Inicial | Aporte Mensal | Juros (0,9% ao mês) | Saldo Acumulado |
|---|---|---|---|---|
| 0 | R$ 100.000,00 | R$ 2.000,00 | – | R$ 102.000,00 |
| 1 | R$ 2.000,00 | R$ 918,00 | R$ 104.918,00 | |
| 2 | R$ 2.000,00 | R$ 943,26 | R$ 107.861,26 | |
| … | ||||
| 119 | R$ 2.000,00 | R$ 10.624,75 | R$ 1.201.535,29 | |
| 120 | R$ 2.000,00 | R$ 10.813,55 | R$ 1.212.345,85 |
Nesta tabela, cada linha representa um mês. A coluna “Investimento Inicial” mostra o saldo acumulado no início do mês. A coluna “Aporte Mensal” mostra o valor adicionado ao saldo no início do mês. A coluna “Juros” mostra o valor dos juros calculados para aquele mês. A coluna “Saldo Acumulado” mostra o saldo total ao final do mês, incluindo o investimento inicial, os aportes mensais e os juros compostos calculados até aquele ponto.
Os cálculos de juros compostos são acumulativos, ou seja, o saldo de cada mês é usado como base para calcular os juros do próximo mês.
Como podemos ver, o investimento com aportes mensais, após 10 anos de rentabilidade, será resgatado com um valor de R$ 1.212.345,85 – uma bela quantia, levando-se em consideração que partimos de R$ 100.000,00.
Além dos R$ 100.000,00 iniciais, foram feitos depósitos mensais de R$ 2000,00, totalizando R$ 240.000,00 em depósitos. Sendo assim, foram aportados R$ 340.000,00 de nosso bolso, e foram recebidos de juros (renda) R$ 1.212.345,85 – R$ 340.000,00 = R$ 872.345,85, bem mais que os aportes em si, mostrando o poder dos juros compostos ao longo do tempo.
